Beating the Vig with AWS

Beating the Vig with AWS
Arbitrage is a term that originates from the world of finance and refers to the practice of taking advantage of price discrepancies in different markets to guarantee a risk-free profit. At its core, it involves buying an asset in one market where the price is low and simultaneously selling it in another market where the price is higher. This principle relies on the assumption that markets are not perfectly efficient, and temporary mispricing can occur. For example, if a stock is trading for 100 dollars on one exchange and 102 dollars on another, an arbitrageur could buy the stock on the cheaper exchange and sell it on the more expensive one, pocketing the 2 dollar difference, all while assuming little to no risk.
Now, imagine applying this concept to sports betting, a world where odds vary across different sportsbooks. We can exploit misaligned prices across different markets just the same. Namely, we can identify mismatched odds between different bookmakers and place multiple bets on the same event, guaranteeing a profit regardless of the outcome.
In this post, I’ll walk through the details of sports-betting arbitrage as well as discuss how I architected an automated system to scan for these opportunities across multiple sportsbooks, alerting subscribers when they arise.
Table of Contents
- Beating the Vig with AWS
Sports Betting: Fundamentals
When it comes to sports betting, odds are the key factor in determining potential payouts. They’re related to the probability of a particular outcome and dictate how much money you can win if that outcome occurs. Books differ in how they convey odds, but three popular formats appear most frequently: decimal, fractional, and American.
Decimal Odds
Decimal odds are commonly used in Europe, Canada and Australia. They represent the total payout (stake & profit) for every dollar wagered. The formula to calculate your total payout is:
$$ \text{Payout} = \text{Stake} \times \text{Odds}. $$
For example, if the odds for a bet are $2.50$ and we bet $10$ dollars, our payout will be:
$$ \text{Payout} = 10 \times 2.50 = 25, $$
meaning that we would win $15$ dollars in profit.
Fractional Odds
More common in the UK, fractional odds are presented as a fraction, like $5/1$ or $10/3$. The numerator represents the amount of profit you will make for every unit staked, while the denominator represents the stake required to win that profit. The formula to calculate the profit is:
$$ \text{Profit} = \text{Stake} \times \text{Odds}. $$
For instance, with $10/3$ odds, if we bet $60$ dollars, our profit would be:
$$ \text{Profit} = 60 \times \left(\frac{10}{3}\right) = 200. $$
Thus, we would receive a total payout of $260$ dollars ($200$ dollar profit plus our $60$ dollar stake).
American Odds
As is American tradition, American Odds (also referred to as “Moneyline Odds”) are often found to be the least intuitive and straightforward units of measurement for new-comers. Popular in the United States, they can either be positive or negative and revolve around a $100$ dollar baseline. Positive odds (assigned to the underdog) show how much profit we would make on a $100$ dollar bet, while negative odds (assigned to the favorite) show how much we need to bet in order to win $100$ dollars.
-
Positive Odds (e.g. $+200$): This means we make a profit of $200$ dollars for every $100$ wagered and:
$$ \text{Profit} = \frac{\text{Stake} \times 200}{100}. $$
For example, a $50$ dollar bet on $+200$ odds would give
$$ \text{Profit} = \frac{50 \times 200}{100} = 100. $$
-
Negative Odds (e.g. $-150$): This means we need to wager $150$ dollars in order to win $100$ dollars and:
$$ \text{Profit} = \frac{\text{Stake}}{|-150|} \times 100. $$
For example, a $75$ dollar bet on $-150$ odds would yield:
$$ \text{Profit} = \frac{75}{150} \times 100 = 50. $$
Remembering how to read and interpret the different conventions for odds formatting may well be the most irritating part of the sports-betting initiation process and to muddy the waters even further: for those statistically-minded individuals out there, you’ll notice that none of these formats directly mirrors what we refer to formally as odds, in the technical sense. Only out of due-diligence did we present three formats here; we’ll choose one to work with throughout the rest of the post. While Moneyline odds are common in th US, we will not be utilizing them nor fractional odds. For their simplicity and convenience with calculations in future sections, we will adopt decimal odds as our convention.
Sports Betting: Arbitrage
Now that we know how to interpret and manipulate odds (the cornerstone of determining payouts, profits and arbitrage opportunities) we may naturally ask how odds are determined and what the necessary & sufficient conditions are for arbitrage opportunities. In order to answer these questions, we must talk about the relationship between betting odds and probabilities.
Implied Probabilities
Let’s take a step back and consider how bookmakers make money. Suppose we want to manage a book to take bets on Team A vs Team B and that we know the true probability of Team A winning is $0.60$. What goes wrong if we set the decimal odds for this line to $2.00$ and $2.00$? A savvy bettor would notice that they can risk a dollar to make a dollar and that more than half of the time, their bet will hit. Thus, their expected profit is:
$$ \mathbb{E}[\text{Profit}] = 0.6 \times 1 + 0.4 \times (-1) = 0.2. $$
In other words, if we were to continue to set odds on $0.60 - 0.40$ probability events equally and this savvy bettor continued to place their bet, they would eventually wind up taking a profit from us. To ensure this doesn’t happen we, instead, set our odds so that the expected profit for bettor and bookmaker is zero. Namely:
$$ \mathbb{E}[\text{Profit}] = P \times (O - 1) + (1 - P) \times (-1) = 0 $$
$$ \implies P \times O - P - 1 + P = 0 $$
$$ \implies P \times O = 1 $$
$$ \implies O = \frac{1}{P} $$
where $P$ is the probability of team A winning and $O$ are the listed odds for team A. Thus, we would set our odds to be $\frac{5}{3} = 1.67$ and $\frac{5}{2} = 2.5$ for team A and team B victories, respectively.
In reality, we want to make a non-zero profit over time. Suppose we collect a total of $1$ dollar in bets on each side (for both team A and B victories). Let’s see what happens if we inflate our probabilities by a factor of $1.05$. Then, team A’s odds become $O_A \approx 1.59$ and team B’s odds become $O_B \approx 2.38$. This means that the expected payout becomes:
$$ \mathbb{E}[\text{Payout}] = 0.6 \times 1.59 + 0.4 \times 2.38 $$
$$ = 1.906 < 2. $$
Thus, we expect to make a profit of $2 - 1.906 = 0.094$, essentially collecting a $9$ cents fee from the pool of bettors. This fee is what is referred to as the “vigorish”, “vig” for short, or, colloquially, the “juice” and is how bookmakers make their money. It is a fee that is built into the odds, rather than charged directly.
Necessary & Sufficient Conditions for Arbitrage
And now, we turn to the heart of the matter: how do we quantify the necessary & sufficient conditions for a sports betting arbitrage opportunity? Let’s intuit based on our conversation about the vig, in the previous section. If scaling up the implied probabilities yields a profit for the bookmaker, we may expect that scaling them down will yield a profit for the bettor. This, in fact, is the case.
Theorem: Assume a sporting event’s outcomes can be partitioned $n$-ways (i.e. there are $n$ mutually exclusive and exhaustive outcomes). Let
- $O_i = $ decimal odds for outcome $i$, where $i = 1, 2, …, n$
- $p_i = $ the implied probability of outcome $i$ occurring
- $S = \sum_{i=1}^n p_i = \sum_{i=1}^n \frac{1}{O_i}$.
Then, there exists an arbitrage opportunity if and only if $S < 1$.
In short, we are looking for instances where the implied probabilities sum to less than $1$.
proof (of Theorem)
Forward Direction
Assume an arbitrage opportunity exists. Without loss of generality, let the total amount of money invested be $1$ dollar and let $x_i$ be the fraction of money bet on outcome $i$ so that $\sum_{i=1}^n x_i = 1$.
By definition, if outcome $i$ occurs, the return is:
$$ \text{Payout} = x_i \times O_i. $$
Since this is an arbitrage opportunity, the payout for each outcome must be greater than $1$. Namely:
$$ x_i \times O_i > 1 $$
$$ \implies x_i > \frac{1}{O_i} $$
for all $i$. Summing both sides of the inequality over $i$ gives:
$$ 1 = \sum_{i=1}^n x_i > \sum_{i=1}^n \frac{1}{O_i} = S. $$
Reverse Direction
Now, assume:
$$ \sum_{i=1}^n \frac{1}{O_i} = S < 1. $$
We need to show that there exists a way to bet on the $n$ outcomes such that the total return is greater than $1$, regardless of the observed outcome. Define
$$ x_i = \frac{\frac{1}{O_i}}{S}. $$
This defines a betting strategy where:
$$ \sum_{i=1}^n x_i = \sum_{i=1}^n \frac{1/O_i}{S} = \frac{1}{S} \times \sum_{i=1}^n \frac{1}{O_i} = 1 $$
so that the total amount bet is equal to $1$. Then, if outcome $i$ occurs, the return in:
$$ x_i \times O_i = \left(\frac{1/O_i}{S}\right) \times O_i = \frac{1}{S} > 1 $$
where the inequality follows from our assumption that $S < 1$.$\blacksquare$
Suppose the odds on Team A vs Team B are $2.10$ and $2.10$ respectively. Then, the implied probabilities would be $\frac{1}{2.10}$ and $\frac{1}{2.10}$, respectively, the sum of which $\approx 0.95 < 1$ and is, thus an arbitrage opportunity. Using the betting strategy outlined in the reverse direction of the above proof, we put:
$$ \frac{\frac{1}{2.10}}{\frac{1}{2.10} + \frac{1}{2.10}} = 0.5 $$
on each team. As expected, this ensures a profit, regardless of the victor, since:
$$ \text{Payout} = 2.10 \times 0.5 = 1.05 $$
which is larger than $1$: the total stake wagered across both bets.
Architecting An Arbitrage Notification System in AWS
Having established the theory behind arbitrage in sports betting, we can now detail how we used cloud resources (specifically in Amazon Web Services) to construct a fully automated detection and notification system.
We utilized the following AWS services:
- Lambda Functions: Three lambda functions with distinct responsibilities.
- Step Function: A step function to orchestrate the execution of the lambda functions.
- Amazon Simple Notification Service (SNS): Pub/Sub service to publish notifications to all subscribers in real-time.
- Amazon EventBridge: Trigger the pipeline to run once every six hours.
- Amazon S3: Durable store for raw API responses and computed arbitrage opportunities.
- AWS Secrets Manager: Securely store API key.
The high-level execution flow is as follows:
- EventBridge fires once every six hours, triggering the
sports-betting-arbitrage-system-expressstep function. - The step function runs three states, in sequence:
sports_betting_arbitrage_query_api: Fetches sportsbook lines and saves the raw JSON response to S3.sports_betting_arbitrage_search_for_arbitrage_opportunity: Processes the API response, checks for opportunities and stores any findings in S3.sports_betting_arbitrage_publish_opportunities: Compares new opportunities with previously published ones and sends notifications via SNS for new opportunities only.
- SNS pushes notifications to all subscribers (in this case, via email).
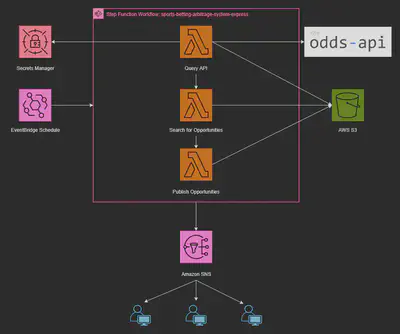
For a detailed view of the source code for each lambda and step function, reference this repository: sports-betting-arbitrage-system (also linked at the top of this page).
Lambda: Query API
As the name suggests, the first Lambda (sports_betting_arbitrage_query_api) is responsible for pulling the latest betting lines from The Odds API.
Key details:
- Secrets Manager stores the API key securely; it is retrieved at runtime.
- Multiple sports and regions can be queried in a single run.
- All requests use decimal odds to simplify downstream calculations.
- The raw API response is timestamped and saved to S3 as JSON.
By storing unprocessed data, we ensure that the system can be re-run or audited at a later date without making additional API calls.
Lambda: Search for Arbitrage Opportunities
The second Lambda (sports_betting_arbitrage_seaerch_for_arbitrage_opportunity) consumes the API response from the first lambda and looks for opportunities using the necessary and sufficient condition derived earlier:
$$ \sum_{i=1}^n \frac{1}{O_i} < 1 $$
def is_arbitrage_opportunity(
decimal_odds_list: list[float]
) -> bool:
implied_probabilities_list = [
1 / odds
for odds in decimal_odds_list
]
total_implied_probabilities = sum(implied_probabilities_list)
if total_implied_probabilities < 1:
return True
return False
def calculate_stake_proportions(
decimal_odds_list: list[float]
) -> list[float]:
implied_probabilities_list = [
1 / odds
for odds in decimal_odds_list
]
total_implied_probabilities = sum(implied_probabilities_list)
return [
(1 / odds) / total_implied_probabilities
for odds in decimal_odds_list
]
Key details:
- Pairwise comparisons are made between books for the same matchup.
- If an arbitrage condition is met, optimal stake proportions are calculated so that the payout is equal regardless of the observed outcome.
- Each opportunity is timestamped and saved to S3 for future reference.
Lambda: Publish New Opportunities
The third and final Lambda (sports_betting_arbitrage_publish_opportunities) determines which opportunities are new relative to the last run, formats them into an email message and publishes this message to the VigVanquisher SNS topic.
Key details:
- AWS S3 is queried for the second-most recent opportunities file. The opportunities therein are compared with the current run’s opportunity list and any net new opportunities are noted.
- Net new opportunities are formatted into an email message, including the bookmaker, matchup, odds, stake proportion, an “as of” date and the calculated payout multiplier. For example, a payout multiplier of $1.10$ means that for every dollar bet on the opportunity, $1.10$ dollars in payout is guaranteed.
- An SNS topic broadcasts the message to all subscribers via email.
Step Function: Orchestrating the Workflow
AWS Step Functions is a serverless workflow orchestration service that enables developers to coordinate multi-step application workflows by defining state machines. These state machines are composed of individual “states” that represent tasks, choices, or other control flow elements. We created a Step Function to operate as the backbone of our system, ensuring that Lambda executes in order and that data flows smoothly from one step to the next.
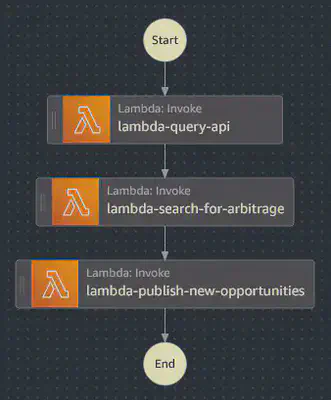
Key details:
- The constraints of our process allow for the use of a Step Function of type “Express” as opposed to “Standard”, introducing significant cost-savings.
- We use JSONata expressions to pass specific fields from one Lambda’s output into the next.
- Includes automatic retries with exponential backoff for transient errors, ensuring resilience.
Step Functions are represented in a JSON-based, structured language called “Amazon States Language” or ASL. The ASL definition is included in the repository here: step_function/sports-betting-arbitrage-system-asl.json.
Simple Notification Service (SNS): Pub/Sub
Finally, a quick word on Amazon SNS, the service we utilize to handle the distribution of arbitrage alerts. Amazon SNS is a fully managed service that provides message delivery from publishers (producers) to subscribers (consumers). Publishers communicate asynchronously with subscribers by sending messages to a topic, which is a logical access point and communication channel.
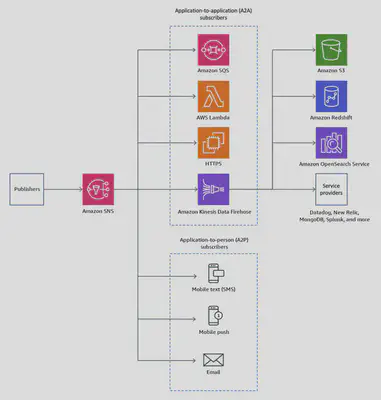
By taking advantage of this Pub/Sub pattern, we decouple the production and consumption components of our pipeline and allow for easy future scaling - both in number of consumers and in forms of notification (SMS, Lambda triggers, webhooks, etc.) - without the need to change upstream logic. Adding users, for example, amounts to a few clicks and entering the recipient address. The recipient will be sent an email prompting them to confirm their subscription, after which they will receive any future published messages.
Conclusion
Building the VigVanquisher system was a rewarding exercise in blending applied statistics, sports analytics, and cloud engineering. By automating the process of fetching odds, detecting arbitrage opportunities, and instantly alerting subscribers, the system demonstrates how modern cloud architectures can turn a theoretical concept into a practical, real-world tool.
While the current implementation focuses on two-outcome arbitrage opportunities in select sports, the foundation is flexible. Future enhancements could include scanning a wider variety of sports, monitoring odds changes closer to real time, generalizing to $n$-outcome opportunities and expanding beyond pure arbitrage by applying machine learning models for odds prediction. These improvements would not only broaden the system’s scope but also deepen its analytical capabilities.
In the end, whether you view it as slaying the “vig” or simply applying statistical rigor to gain an edge, this project highlights the power of combining domain expertise with cloud-based automation. The thrill lies not just in finding opportunities, but in building the tools that make finding them possible.